NCERT Class 10 Science Chapter 9 Light : Reflection and Refraction Question Answer Solution For School Students of Class 10th. We also Provides Notes and Important Questions for Class 10 Science. NCERT Class 10th Science book is applied in mostly boards like CBSE, HBSE, RBSE, Up Board, MP Board and also some other state boards.
- Also Read:- Class 10 Science NCERT Solution
- Also Read – Class 10 Important Questions
NCERT Class 10 Science Chapter 9 Light : Reflection and Refraction Question Answer (Textual + Internal) for CBSE, HBSE, RBSE, UK Board, HP Board, MP Board and Other Boards Solution.
NCERT Class 10 Science Chapter 9 Question Answer (Textual + Internal)
Internal Questions from Page 142
Q1. Define the principal focus of a concave mirror.
Ans. A number of rays parallel to principal axis of concave mirror after reflection meets at a point on principal axis. This point is called principal focus. It is represented by F.
Q2. The radius of curvature of a spherical mirror is 20 cm. What is its focal length?
Ans. Given, Radius of curvature R = 20 cm, focal length f = ?
Using, R = 2f
20 = 2f
f = 10 cm
Q3. Name a mirror that can give an erect and enlarged image of an object.
Ans. Concave mirror
Q4. Why do we prefer a convex mirror as a rear-view mirror in vehicles?
Ans. Convex mirrors are commonly used as rear-view (wing) mirrors in vehicles becasue these mirrors enables the driver to see the traffic behind him/her to facilitate the safe driving. Convex mirror always give erect and diminished image and give wider view as they are curved outwards.
Internal Questions from Page 145
Q1. Find the focal length of a convex mirror whose radius of curvature is 32 cm.
Ans. Given, Radius of curvature R = 32 cm, focal length f = ?
Using, R = 2f
32 = 2f
f = 16 cm
Therefore, required focal length is 16 cm.
Q2. A concave mirror produces three times magnified (enlarged) real image of an object placed at 10 cm in front of it. Where is the image located?
Ans. Magnification produced by a spherical mirror :
Let the height of object h
Then, height of image = – 3h
Object distance (u) = – 10 cm
v = 3(-10) = – 30 cm
The negative sign indicates that an inverted image is formed in front of the given concave mirror at a distance of 30 cm.
Internal Questions from Page 150
Q1. A ray of light travelling in air enters obliquely into water. Does the light ray bend towards the normal or away from the normal? Why?
Ans. The light ray will bend towards the normal. Because when a light ray enter from rarer to denser medium its speed decreases and it bends towards normal. Similar is in this case. Water is optically denser than air. On entering water, the speed of light decreases and the light bends towards normal.
Q2. Light enters from air to glass having refractive index 1.50. What is the speed of light in the glass? The speed of light in vacuum is 3 × 108 m s–1 .
Ans. Let the speed of light in the glass be x m s–1.
Using,
Refractive index of transparent medium = Speed of light in vacuum / speed of light in medium
1.50 =
x =
x = 2 × 108 ms–1
Q3. Find out, from Table 9.3, the medium having highest optical density. Also find the medium with lowest optical density.
Ans. From the given table,
Lowest optical density = Air
Highest optical density = Diamond
Q4. You are given kerosene, turpentine and water. In which of these does the light travel fastest? Use the information given in Table 9.3.
Ans. Speed of light is greater in medium which having low refractive index. On comapring, we get water has lowest refractive index among all. Therefore, speed of light will be fastest in water among given mediums.
Q5. The refractive index of diamond is 2.42. What is the meaning of this statement?
Ans. The above statement means that the speed of light in diamond is 1/2.42 times the speed of light in vacuum.
Internal Questions from Page 158
Q1. Define 1 dioptre of power of a lens.
Ans. Dioptre is the SI unit of power of a lens. 1 Diopte can be defined as the power of a lens of focal length 1 metre. Dioptre is denoted by D.
Q2. A convex lens forms a real and inverted image of a needle at a distance of 50 cm from it. Where is the needle placed in front of the convex lens if the image is equal to the size of the object? Also, find the power of the lens.
Ans. Position of image should be at 2F since the image is real and of the same size.
Given, object distance (u) = – 50 cm
Image distance (v) = 50 cm
Focal length = f
Using lens formula ,
f = 25 cm = 0.25m
Power of lens, P = 1/f = 1/0.25 = + 4D
Q3. Find the power of a concave lens of focal length 2 m.
Ans. Given, Focal length = 2m
Power of lens P =1/f
Focal length of concave mirror is always negative .
Therefore,
P = 1/(-2) = -0.5 D
Textual Exercise Question Answer
Q1. Which one of the following materials cannot be used to make a lens?
(a) Water
(b) Glass
(c) Plastic
(d) Clay
Ans. (d) Clay
Q2. The image formed by a concave mirror is observed to be virtual, erect and larger than the object. Where should be the position of the object?
(a) Between the principal focus and the centre of curvature
(b) At the centre of curvature
(c) Beyond the centre of curvature
(d) Between the pole of the mirror and its principal focus.
Ans. (d) Between the pole of the mirror and its principal focus.
Q3. Where should an object be placed in front of a convex lens to get a real image of the size of the object?
(a) At the principal focus of the lens
(b) At twice the focal length
(c) At infinity
(d) Between the optical centre of the lens and its principal focus.
Ans. (b) At twice the focal length
Q4. A spherical mirror and a thin spherical lens have each a focal length of –15 cm. The mirror and the lens are likely to be
(a) both concave.
(b) both convex.
(c) the mirror is concave and the lens is convex.
(d) the mirror is convex, but the lens is concave.
Ans. (a) both concave.
Q5. No matter how far you stand from a mirror, your image appears erect. The mirror is likely to be
(a) only plane.
(b) only concave.
(c) only convex.
(d) either plane or convex
Ans. (d) either plane or convex
Q6. Which of the following lenses would you prefer to use while reading small letters found in a dictionary?
(a) A convex lens of focal length 50 cm
(b) A concave lens of focal length 50 cm
(c) A convex lens of focal length 5 cm
(d) A concave lens of focal length 5 cm
Ans. (c) A convex lens of focal length 5 cm
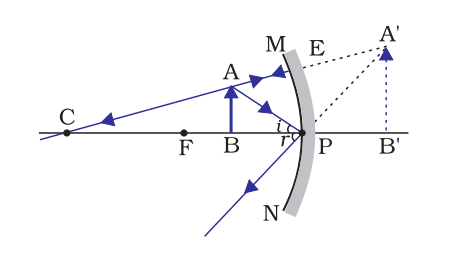
Q7. We wish to obtain an erect image of an object, using a concave mirror of focal length 15 cm. What should be the range of distance of the object from the mirror? What is the nature of the image? Is the image larger or smaller than the object?
Draw a ray diagram to show the image formation in this case.
Ans. A concave mirror gives an erect image when object is place between focus F and pole P.
As we have given focal length 15 cm. Therefore, range of object will be 0 to 15 cm from the pole of the mirror.
The image formed will be virtual, erect and larger than the object.
Q8. Name the type of mirror used in the following situations.
(a) Headlights of a car.
(b) Side/rear-view mirror of a vehicle.
(c) Solar furnace.
Support your answer with reason.
Ans. (a) Concave mirrors are headlights of cars to get powerful parallel beams of light of light when the light source is placed at their principal focus.
(b) Convex mirror is used as side/rear view mirror of a vehicle because of its largest field of view.
(c) Concave mirror : Large concave mirrors are used to concentrate sunlight to produce heat in solar furnaces.
Q9. One-half of a convex lens is covered with a black paper. Will this lens produce a complete image of the object? Verify your answer experimentally. Explain your observations.
Ans. Yes, it will produce complete image of the object but the intensity or brightness of the image will reduce. This can be verified experimentally by observing the image of a distant object, like a tree on a screen, when the one half of the lens is covered with black paper.
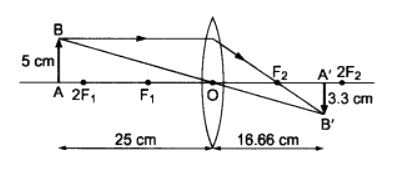
Q10. An object 5 cm in length is held 25 cm away from a converging lens of focal length 10 cm. Draw the ray diagram and find the position, size and the nature of the image formed.
Ans. Given, Height of object, ho = 5 cm
Distance of the object from converging lens, u = – 25 cm
Focal length of converging lens, f = 10 cm
Using lens formula,
v = 50/3 = 16.67 cm
Also, for a converging lens,
hi = -10/3 = 3.3 cm
Therefore, the image formed is inverted and at a distance of 16.67 cm behind the lens and measures 3.3 cm.
Ray diagram is given below :
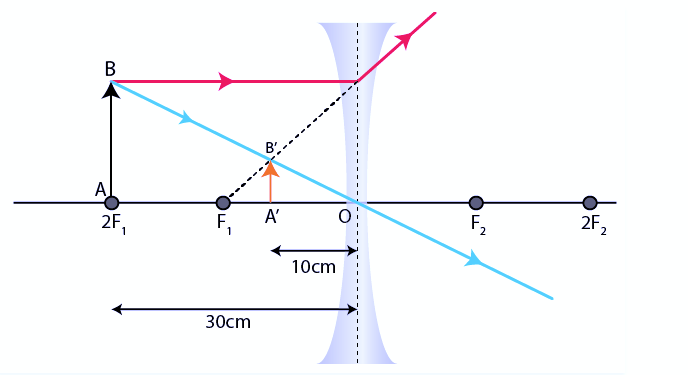
Q11. A concave lens of focal length 15 cm forms an image 10 cm from the lens. How far is the object placed from the lens? Draw the ray diagram.
Ans. Given, focal length f = – 15 cm, Image distance, v = -10 cm, Object distance, u = ?
Using lens formula,
u = -30 cm
Therefore, object is placed 30 cm in front of the lens.
Q12. An object is placed at a distance of 10 cm from a convex mirror of focal length 15 cm. Find the position and nature of the image.
Ans. Given,
Object distance, u = -10 cm, Focal length, f = +15 cm, Image distance, v = ?
Using Mirror formula,
v = 6 cm
Thus, image is virtual and is formed behind the mirror at a distance of 6cm.
Magnification of mirror, m =
m =
Therefore, positive value of magnification shows that image formed is erect and as value of m is less than 1, it shows that image is smaller than the object.
Thus, image is virtual, erect and diminished.
Q13. The magnification produced by a plane mirror is +1. What does this mean?
Ans. Positive sign in magnification means image formed by plane mirror is virtual and erect. And magnification is 1 means height of image is equal to the height of object.
Q14. An object 5.0 cm in length is placed at a distance of 20 cm in front of a convex mirror of radius of curvature 30 cm. Find the position of the image, its nature and size.
Ans. Given object size, ho = +5 cm
Object distance, u = – 20 cm
Radius of curvature, R = 30 cm
Focal length, f = R/2 = 30/2 = 15 cm
Using mirror formula,
v = 60/7 = 8.6 cm
Magnification of mirror, m =
hi = = 2.15 cm
Therefore, a virtual, erect image of height 2.15 cm is formed behind the mirror at a distance of 8.6 cm from the mirror.
Q15. An object of size 7.0 cm is placed at 27 cm in front of a concave mirror of focal length 18 cm. At what distance from the mirror should a screen be placed, so that a sharp focused image can be obtained? Find the size and the nature of the image.
Ans. Given , object size, ho = +7 cm
Object distance, u = -27 cm , focal length, f = -18 cm
Image distance, v = ?, Image size, hi = ?
Using mirror formula,
v = -54 cm
Therefore, the screen should be placed at a distance of 54 cm in front of mirror .
Magnification of mirror, m =
hi = – 14 cm
The image is real, inverted and enlarged in size.
Q16. Find the focal length of a lens of power – 2.0 D. What type of lens is this?
Ans. Power of lens P = 1/f
-2.0 = 1/f
f = 1/(-2) = -0.5 m
Concave lens has negative focal length. Therefore, given lens is concave.
Q17. A doctor has prescribed a corrective lens of power +1.5 D. Find the focal length of the lens. Is the prescribed lens diverging or converging?
Ans. Power of a lens P = 1/f
1.5 = 1/f
f = 1/1.5
f = 2/3 m
Since convex lens has positive focal length. Therefore, convex lens is used. And we know that convex lens is converging in nature.
Therefore, prescribed lens is converging in nature.