HBSE Class 9 गणित Important Question Answer 2026

Most of students search over Google for Haryana Board (HBSE) Important Questions 2026. Here is the Main reason because HBSE Board Says that in HBSE Exam 2026 (last 3 Years of Questions will Repeat) so that here are the selected List of Questions of Haryana Board For Class 12.

HBSE Class 9 गणित Important Question Answer 2026

Chapter 1 – संख्या पद्धति

प्रश्न 1. $\displaystyle 0.\overline{{47}}$ का $\displaystyle \frac{p}{q}$ रूप _________ है।

प्रश्न 2. $\displaystyle \frac{1}{{7+3\sqrt{2}}}$ के हर का परिमेयकरण कीजिए।

प्रश्न 3. $\displaystyle \frac{5}{{\sqrt{3}-\sqrt{5}}}$ के हर का परिमेयकरण कीजिए।

प्रश्न 4. $\displaystyle \frac{1}{{\sqrt{5}+\sqrt{2}}}$ के हल का परिमेयकरण करने पर क्या प्राप्त होगा ?

प्रश्न 5. $\displaystyle (3+\sqrt{3})(2+\sqrt{2})$ का मान है।

प्रश्न 6. 3 और 4 के बीच एक परिमेय संख्या बताएँ ।

प्रश्न 7. प्रत्येक परिमेय संख्या एक पूर्णांक होती है। (सत्य/असत्य)

प्रश्न 8. सरल कीजिए : $\displaystyle (3+\sqrt{3})(3-\sqrt{3})$

प्रश्न 9. सरल कीजिए: $\displaystyle {{2}^{{\frac{2}{3}}}}{{.2}^{{\frac{1}{5}}}}$

प्रश्न 10. 0.3333 …… = $\displaystyle 0.\overline{3}$ को $\displaystyle \frac{p}{q}$ , के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।

प्रश्न 11. 0.99999 _______ को $\displaystyle \frac{p}{q}$ के रूप व्यक्त कीजिए।

प्रश्न 12. $\displaystyle 0.\overline{6}$ को $\displaystyle \frac{p}{q}$ के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।

Chapter 2 – बहुपद

प्रश्न 1. द्विघात बहुपद 6x² + 5x – 6 के गुणनखण्ड ज्ञात कीजिए।

प्रश्न 2. गुणनखण्ड कीजिए : 27x³ + y³ + z³ – 9xyz

प्रश्न 3. गुणनखण्ड कीजिए : 64m³ – 343m³

प्रश्न 4. गुणनखण्ड कीजिए : $\displaystyle \frac{{{{x}^{2}}}}{{100}}-{{y}^{2}}$

प्रश्न 5. गुणनखंड कीजिए: 8a³ + b³ + 12a²b + 6ab²

प्रश्न 6. सीधे गुणा किए बिना 103 x 107 का मान ज्ञात कीजिए।

प्रश्न 7. गुणनखण्ड कीजिए : 4x² + 9y² + 16z² + 12xy – 24yz – 16xz

प्रश्न 8. गुणनखण्ड कीजिए: x³ + 13x² + 32x + 20

प्रश्न 9. गुणनखण्ड ज्ञात कीजिए : x³ – 2x² – x + 2

प्रश्न 10. सर्वसमिका का प्रयोग करके 103 x 107 का मान ज्ञात करें।

प्रश्न 11. वास्तव में घनों का परिकलन किए बिना (28)³ + (−15)³ + (−13)³ का मान ज्ञात कीजिए।

प्रश्न 12. उपयुक्त सर्वसमिका का प्रयोग करके (102)² का मान ज्ञात कीजिए।

प्रश्न 13. k का मान ज्ञात कीजिए जब x – 1 बहुपद x² + x + k का एक गुणनखण्ड हो ।

प्रश्न 14. p(x) = 3x + 1 का शून्यक ________ है

प्रश्न 15. 2 – x² +x³ में x² का गुणांक ________ है :

प्रश्न 16. 64m³ – 343n³ के गुणनखण्ड __________ है।

प्रश्न 17. (x + 4) (x + 10) का गुणनफल क्या है ?

प्रश्न 18. $\displaystyle {{[x-\frac{2}{3}y]}^{{-3}}}$ को प्रसारित रूप में लिखिए।

Q19. k का मान ज्ञात कीजिए, यदि x = 2, y = 1 समीकरण 2x + 3y = k का एक हल हैं ।

Q20. k का मान ज्ञात कीजिए यदि x – 1, P(x) का गुणनखण्ड है P(x) = 2x² + kx + √2

Q21. गुणनखण्ड प्रमेय से x² – 5x + 6 का गुणनखण्डन कीजिए।

Q22. गुणनखण्ड कीजिए: 2x² + 7x + 3

Q23. गुणनखण्ड कीजिए: 64x³– 343y³

Q24. गुणनखण्ड कीजिए : 8x³ + y³ + 27z³ – 18xyz

Chapter 3 – निर्देशांक ज्यामिति

प्रश्न 1. किस चतुर्थांश में या किस अक्ष पर बिंदु (-2, 4), (3, −1), (−1, 0), (1, 2) स्थित हैं। कार्तीय तल पर इनका स्थान निर्धारण करके अपने उत्तर को सत्यापित कीजिए ।

प्रश्न 2. निम्नलिखित संख्या युग्मों को कार्तीय तल के बिन्दुओं के रूप में आलेखित कीजिए :

x	-2	-3	3	0
y	-3	7	-1	-1.5

प्रश्न 3. निम्नलिखित संख्या युग्मों को कार्तीय तल के बिन्दुओं के रूप में आलेखित कीजिए :

x	3	-2	-1	1
y	-1	6	-4	-3

प्रश्न 4. कार्तिये तल में क्षैतिज और ऊर्ध्वाधर रेखाओं से बने तल के प्रत्येक भाग का नाम लिखिए।

प्रश्न 5. बिन्दु (5, -7) कौन-से चतुर्थाश में है ?

प्रश्न 6. बिन्दु (0, 0) जहाँ x-अक्ष और y-अक्ष परस्पर प्रतिच्छेद करते हैं, उसे _______ कहते हैं।

प्रश्न 7. बिन्दु (6, -4) का भुज और कोटि _________ है।

प्रश्न 8.

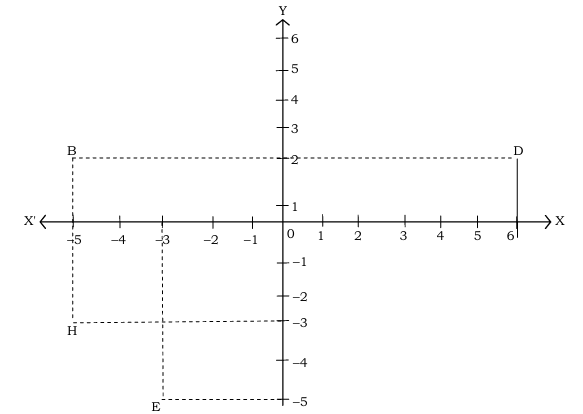
आकृति में देखकर निम्नलिखित को लिखिए :

(i) B के निर्देशांक

(ii) निर्देशांक (-3, 5) द्वारा पहचाना गया बिंदु

(iii) बिंदु D का भुज

(iv) बिंदु H के निर्देशांक

प्रश्न 9.

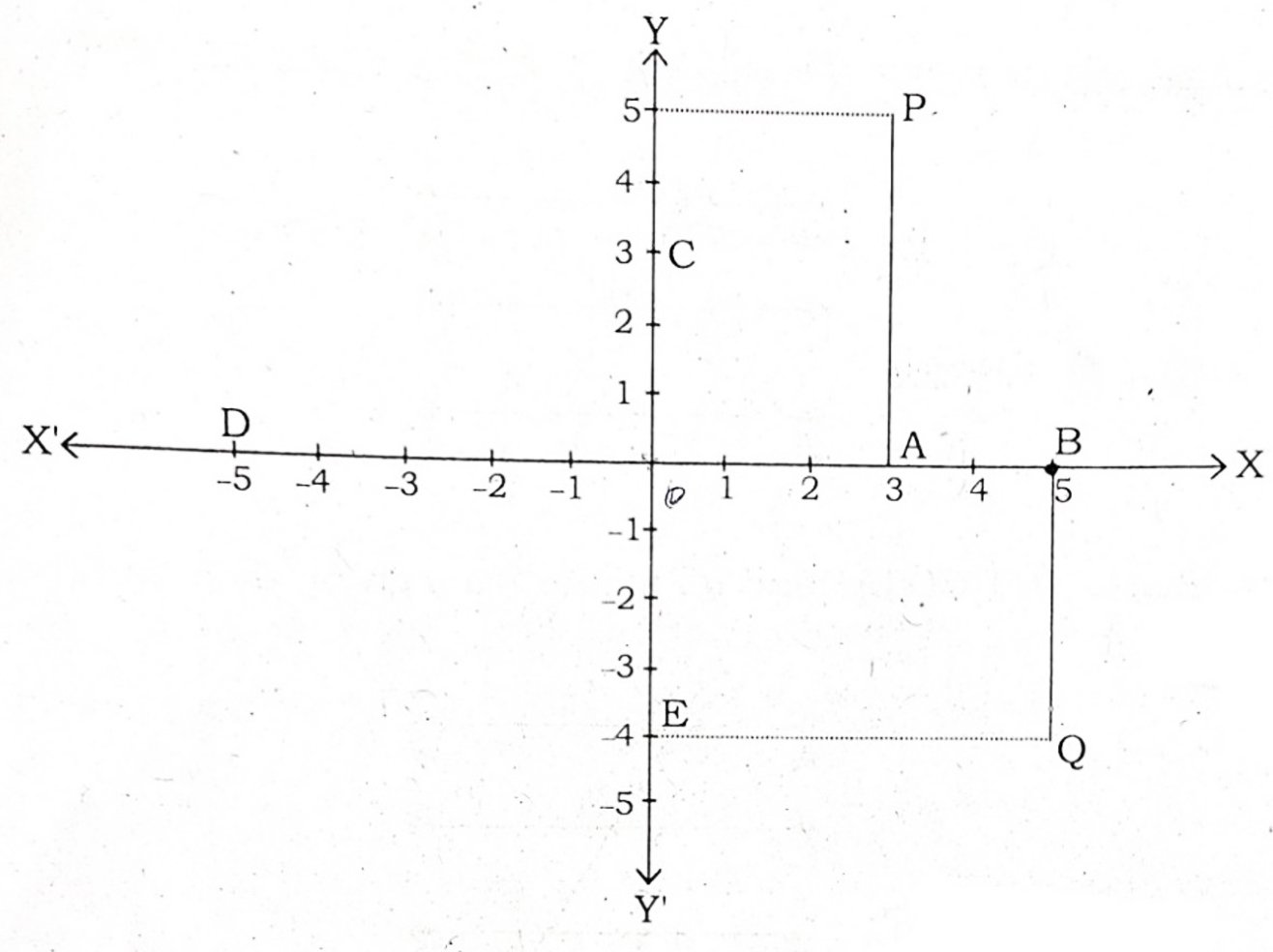
उपरोक्त आकृति देखकर निम्न प्रश्नों के उत्तर दीजिए :

(i) A, B, C, D, E के निर्देशांक

(ii) बिन्दु D का भुज

(iii) बिन्दु E की कोटि

(iv) P, Q के निर्देशांक

Chapter 4 – दो चरो वाले रैखिक समीकरण

प्रश्न 1. समीकरण 2x + y = 7 के चार हल लिखिए।

प्रश्न 2. एक आयताकार हाल के फर्श का परिमाप 250m है यदि ₹ 12 प्रति m² की दर से चारों दीवारों पर पेंट करवाने का व्यय ₹18,000 है, तो हाल की ऊँचाई ज्ञात कीजिए।

प्रश्न 3. समीकरण (2x + 1) = x + 3 का क्या हल है ?

प्रश्न 4. समीकरण 2x + 1 = x – 3 को हल कीजिए और हल को (i) संख्या रेखा पर, (ii) कार्तीय तल पर निरूपित कीजिए।

प्रश्न 5. समीकरण 2x + 8 = 0 को हल कीजिए और हल को (i) संख्या रेखा पर (ii) कार्तीय तल पर निरूपित कीजिए।

प्रश्न 6. समीकरण x + 2y = 6 के चार अलग-अलग हल ज्ञात कीजिए।

प्रश्न 7. P का मान ज्ञात कीजिए जबकि x = 2 , y = 1 समीकरण 2x +3y =P का एक हल हो ।

प्रश्न 8. एक रैखिक समीकरण पर तब कोई प्रभाव नहीं पड़ता जबकि समीकरण के दोनों पक्षों में समान संख्या जोड़ी या घटाई जाती है। (सत्य / असत्य)

Ans – सत्य

Chapter 5 – यूक्लिड की ज्यामिति का परिचय

प्रश्न 1. यूक्लिड की दूसरी अभिधारणा क्या है ?

प्रश्न 2. यूक्लिड की पहली अभिधारणा लिखिए।

Ans – एक बिंदु से एक अन्य बिंदु तक एक सीधी रेखा खींची जा सकती है।

प्रश्न 3. यदि चित्र में AC = BD है, तो सिद्ध कीजिए AB = CD : Most Important

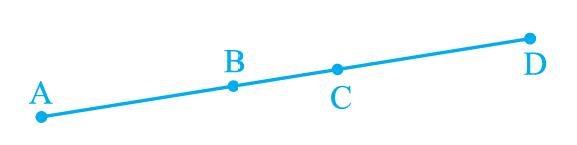
Chapter 6 – रेखाएं और कोण

प्रश्न 1. उस बिंदु का नाम बताइए जहाँ से दो रेखाएँ प्रतिच्छेदित होती है।

प्रश्न 2. निम्नलिखित पदों में से प्रत्येक की परिभाषा दीजिए : (i) समांतर रेखाएँ (ii) रेखाखंड

प्रश्न 3. संपूरक कोण को परिभाषित कीजिए। इसके कोई दो उदाहरण भी दीजिए।

प्रश्न 4. दी गई आकृति में यदि AB || CD|| EF और y : z = 3: 7 है, तो x का मान ज्ञात कीजिए |

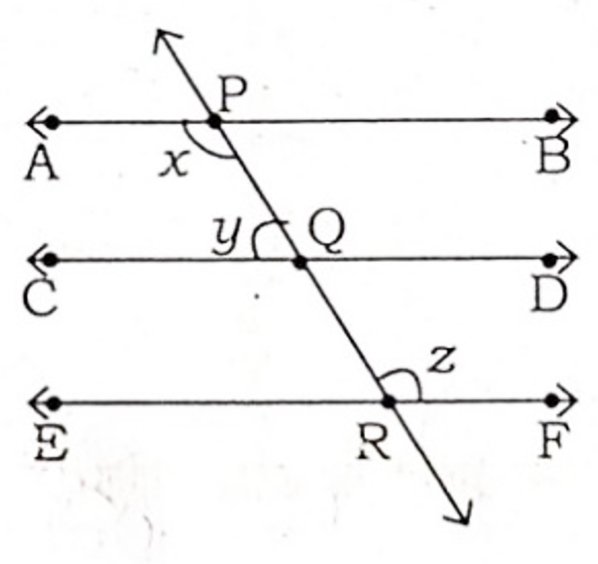
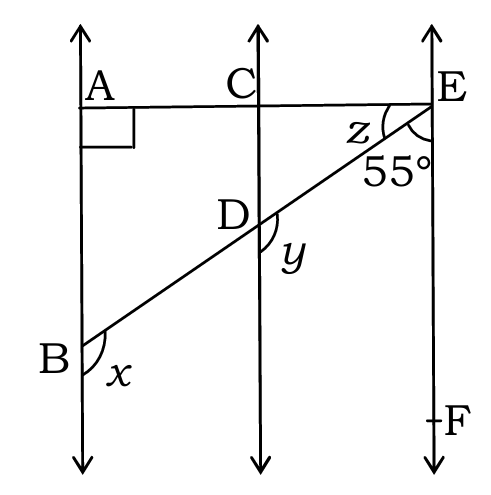
प्रश्न 5. आकृति में, AB||CD और CD||EF है। साथ ही EA ⊥ AB है। यदि ∠BEF 55° है, तो x, y और z के मान ज्ञात कीजिए।

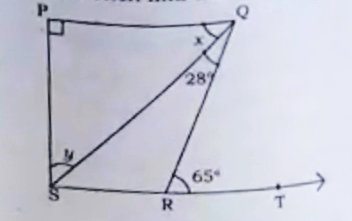
प्रश्न 6. आकृति में यदि PQ ⊥ PS, PQ || SR, ∠SQR = 28° और ∠QRT = 65° है, तो x और y के मान ज्ञात कीजिए :

प्रश्न 7. एक सांत रेखा को अनिश्चित रूप से बढ़ाया जा सकता है। (सत्य / असत्य)

Chapter 7 – त्रिभुज

प्रश्न 1. सिद्ध कीजिए कि एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।

प्रश्न 2. दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।

प्रश्न 3. एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 8 सेमी, ∠B = 45° और AB – AC = 3.5 सेमी हो।

प्रश्न 4. ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि :

(i) D भुजा AC का मध्य बिंदु है।

(ii) MD ⊥ AC है

(iii) CM = MA = $\displaystyle \frac{1}{2}$ AB है

प्रश्न 5. एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 7 सेमी, ∠B = 75° और AB + AC = 13 सेमी हो।

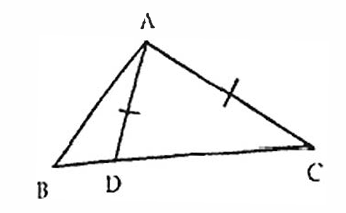
प्रश्न 6. ΔABC की भुजा BC पर D एक ऐसा बिन्दु है कि AD = AC दर्शाइए कि AB > AD

प्रश्न 7. ΔABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C का मान क्या होगा ?

प्रश्न 8. यदि ΔPRQ ≅ ΔCBA हो, तो बताइए :

(i) QR =________

(ii) PR =________

(iii) PO = ________

(iv) ∠B =________

प्रश्न 9. समद्विबाहु त्रिभुज की भुजाओं के मध्य बिन्दुओं को मिलाने से निर्मित त्रिभुज ________ होता है।

प्रश्न 10. दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।

प्रश्न 11. किसी त्रिभुज की रचना के लिए उसके कम से कम _________ भाग दिए होने चाहिए।

प्रश्न 12. त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से ___________ होता है।

Chapter 8 – चतुर्भुज

प्रश्न 1. सिद्ध कीजिए कि चक्रीय समांतर चतुर्भुज आयत होता है।

प्रश्न 2. दिखाइए कि समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।

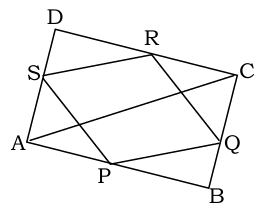
प्रश्न 3. ABCD एक चतुर्भुज है। जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य बिंदु हैं। AC उसका एक विकर्ण है, दर्शाइए कि

(i) SR || AC और SR = $\displaystyle \frac{1}{2}$ AC हैं

(ii) PO = SR हैं

(iii) PQRS एक समांतर चतुर्भुज है।

प्रश्न 4. यदि किसी चक्रीय चतुर्भुज की दो भुजाएँ समांतर हो, तो सिद्ध कीजिए कि

(i) शेष दोनों भुजाएँ बराबर हैं और

(ii) दोनों विकर्ण बराबर है

प्रश्न 5. दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखंड परस्पर समद्विभाजित करते हैं।

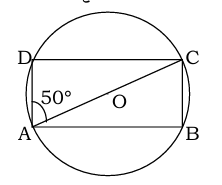
प्रश्न 6. एक चक्रीय चतुर्भुज ABCD में AOC वृत्त का व्यास है। यदि ∠CAD = 50° हो, तो ∠ACD का मान क्या है ?

प्रश्न 7. एक आयत के विकर्ण _______ होते हैं।

प्रश्न 8. यदि एक चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करें, तो वह एक समान्तर चतुर्भुज होता है। (सत्य/असत्य)

Chapter 9 – वृत्त

Q1. सिद्ध कीजिए कि चक्रीय समांतर चतुर्भुज एक आयत है।

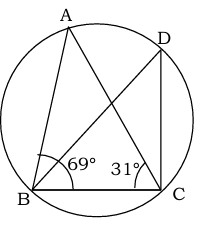
प्रश्न 2. आकृति में ∠ABC = 69° और ∠ACB =31° हो तो ∠BDC ज्ञात कीजिए।

प्रश्न 3. एक रोलर (Roller) का व्यास 84 सेमी है और लम्बाई 120 सेमी है। एक खेल के मैदान को एक बार समतल करने के लिए 500 चक्कर लगाने पड़ते हैं। खेल के मैदान का मी०² में क्षेत्रफल ज्ञात कीजिए।

प्रश्न 4. एक ही वृत्तखंड के कोण ______ होते हैं।

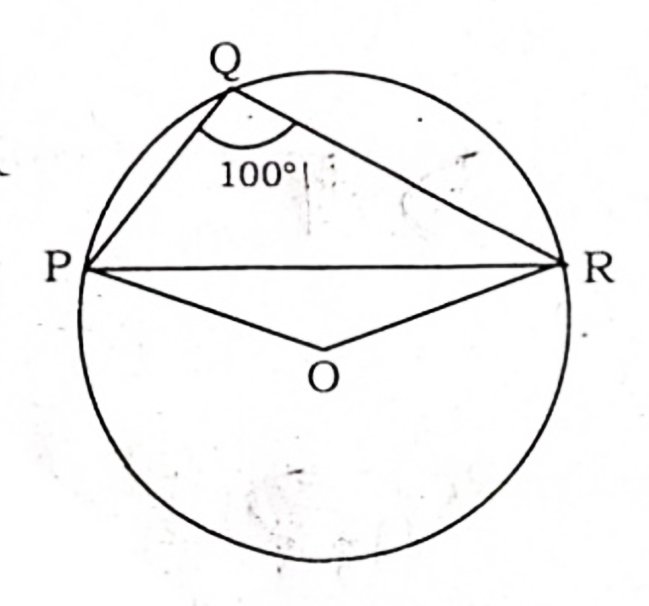
प्रश्न 5. दी गई आकृति में ∠POR = 100° है, जहाँ बिन्दु P, Q तथा R केन्द्र O वाले एक वृत्त पर स्थित हैं। ∠OPR ज्ञात कीजिए ।

प्रश्न 6. आकृति में, केन्द्र वाले एक वृत्त पर तीन बिंदु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° हैं। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है, तो ∠ADC होगा :

प्रश्न 7. एक वृत्त में समान लम्बाई की परिमितं जीवाएँ होती हैं। (सत्य / असत्य)

Chapter 10 – हीरोन का सूत्र

प्रश्न 1. उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 सेमी और 10 सेमी है तथा उसका परिमाप 42 सेमी है।

प्रश्न 2. उस त्रिभुजाकार भूखंड का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओं का अनुपात 3 : 5 : 7 है और उसका परिमाप 300 मी० है।

Chapter 11 – पृष्ठीय क्षेत्रफल और आयतन

प्रश्न 1. लंब वृत्तीय शंकु का आयतन ज्ञात कीजिए जिसकी त्रिज्या 6 cm और ऊंचाई 7 cm है।

प्रश्न 2. एक शंकु की ऊँचाई 15 सेमी है। इसका आयतन 1570 सेमी³ है। इसकी आधार की त्रिज्या क्या होगी ?

प्रश्न 3. एक लंब वृत्तीय शंकु का आयतन 9856 cm³. है। यदि इसके आधार का व्यास 28 cm है, तो ज्ञात कीजिए :
(i) शंकु की ऊँचाई
(ii) शंकु की तिर्यक ऊँचाई
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल

प्रश्न 4. शंकु के आकार का एक तंबू 10 मी० ऊँचा है और उसके आधार की त्रिज्या 24 मी० है। ज्ञात कीजिए

(i) तंबू की तिर्यक ऊँचाई।

(ii) तंबू में लगे कैनवास की लागत, यदि 1 मी० कैनवास की लागत ₹ 70 है।

प्रश्न 5. एक वृत्ताकार कुएँ का आंतरिक व्यास 3.5 मी है और यह 10 मी गहरा है। ज्ञात कीजिए

(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल।

(ii) ₹40 प्रति मी² की दर से इसके वक्र पृष्ठ पर प्लास्टर कराने का व्यय।

प्रश्न 6. अर्धगोला का आयतन जिसकी त्रिज्या r है वो _______ होगा।

प्रश्न 7. त्रिज्या 21 सेमी वाले एक अर्धगोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

प्रश्न 8. उस गोले की त्रिज्या ज्ञात कीजिए, जिसका पृष्ठीय क्षेत्रफल 154 सेमी² है।

Chapter 12 – सांख्यिकी

प्रश्न 1. नीचे दी गयी सारणी में 400 नियॉन लैम्पों के जीवन-काल दिए गए है

जीवन काल (घंटो‌ में)

लैम्पों की‌ संख्या

300-400

400-500

500-600

600-700

700-800

800-900

900-1000

(i) एक आयत चित्र की सहायता से दी हुई सूचनाओं को निरूपित कीजिए।

(ii) कितने लैम्पों के जीवन काल 700 घंटों से अधिक है ?

प्रश्न 2. नौंवी कक्षा के 30 विद्यार्थियों के रक्त समूह निम्न हैं:

A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O

इन आँकड़ों को एक बारंबारता बंटन सारणी के रूप में प्रस्तुत कीजिए।

प्रश्न 3. एक परिवार की मासिक आय ₹6,400 है। विभिन्न मदों के अंतर्गत हर महीने होने वाले खर्च की योजना इस प्रकार बनाई गई है :

ग्रॉसरी	कपड़े	शिक्षा	विविध	बचत
2100	600	1200	1500	1000

(i) उपरोक्त आँकड़ों के लिए दंड-आलेख बनाइए ।

(ii) किस मद पर सबसे अधिक खर्च किया गया है ?

प्रश्न 4. वर्ग 140-150 का वर्ग चिह्न _______ है।