HBSE Class 9 गणित MCQ Important Question Answer 2026

Most of students search over Google for Haryana Board (HBSE) Important Questions 2026. Here is the Main reason because HBSE Board Says that in HBSE Exam 2026 (last 3 Years of Questions will Repeat) so that here are the selected List of Questions of Haryana Board For Class 12.

HBSE Class 9 गणित MCQ Important Question Answer 2026

Chapter 1 – संख्या पद्धति

1. निम्नलिखित संख्याओं में अपरिमेय संख्या कौन-सी है ?
(A) $\displaystyle \sqrt{{16}}$
(B) $\displaystyle \sqrt{{36}}$
(C) $\displaystyle \sqrt{{48}}$
(D) $\displaystyle \sqrt{{64}}$

Ans – (C) $\displaystyle \sqrt{{48}}$

2. (36)^1/2 का मान होगा :
(A) 6
(B) 12
(C) 18
(D) 9

Ans – (A) 6

3. नीचे दिए गए कथनों में से कौन-सा सत्य है ?
(A) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
(B) प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है।
(C) एक परिमेय संख्या है।
(D) $\displaystyle \sqrt{{25}}$ एक अपरिमेय संख्या होती है।

Ans – (A) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।

4. निम्नलिखित में से अपरिमेय संख्या कौन-सी है ?
(A) 5.764
(B) 5.676776777….
(C) $\displaystyle \sqrt{{36}}$
(D) 5.764764…….

Ans – (B) 5.676776777….

5. प्रत्येक पूर्णाक एक परिमेय संख्या होता है।
(A) सत्य
(B) असत्य
(C) कभी-कभी, हमेशा नहीं
(D) इनमें से कोई नहीं

Ans – (A) सत्य

6. परिमेय संख्याओं के संग्रह को अंग्रेजी के किस शब्द द्वारा प्रकट करते हैं ?
(A) N
(B) W
(C) Q
(D) Z

Ans – (C) Q

7. 1 और 2 के बीच की परिमेय संख्या होगी :

(A) 0.5

(B) $\displaystyle \frac{1}{6}$

(D) $\displaystyle \frac{3}{2}$

Ans – (D) $\displaystyle \frac{3}{2}$

8. किन्हीं दो दी हुई परिमेय संख्याओं के बीच कितनी परिमेय संख्याएँ होती हैं ?
(A) 2
(B) 1
(C) अपरिमित रूप से अनेक
(D) 0

Ans – (C) अपरिमित रूप से अनेक

9. निम्नलिखित संख्याओं में कौन-सी अपरिमेय संख्या है ?
(A) 1.101001000…….
(B) 0.376
(C) 0.7474
(D) $\displaystyle \sqrt{{225}}$

Ans – (A) 1.101001000…….

10. निम्न में से कौन-सी परिमेय संख्या नहीं है ?
(A) $\displaystyle \sqrt{2}$
(B) 0
(C) $\displaystyle \sqrt{4}$
(D) $\displaystyle \sqrt{{-16}}$

Ans – (A) $\displaystyle \sqrt{2}$

11. निम्नलिखित में से कौन-सी संख्या $\displaystyle \frac{4}{5}$ और $\displaystyle \frac{9}{5}$ के बीच में नहीं है ?

(A) $\displaystyle \frac{3}{5}$

(B) $\displaystyle \frac{5}{5}$

(D) $\displaystyle \frac{8}{5}$

Ans – (A) $\displaystyle \frac{3}{5}$

12. 16^3/4 का मान है :
(A) 4
(B) 12
(C) 8
(D) 48

Ans – (C) 8

13. $\displaystyle 0.\overline{{001}}$ का $\displaystyle \frac{p}{q}$ होगा :

(A) $\displaystyle \frac{1}{{999}}$

(B) $\displaystyle \frac{1}{{9}}$

(D) $\displaystyle \frac{1}{{9999}}$

Ans – (A) $\displaystyle \frac{1}{{999}}$

Chapter 2 – बहुपद

1. निम्नलिखित बीजीय व्यंजकों में कौन-सा एक बहुपद है ? 1
(A) x² + 5x + 6
(B) $\displaystyle y+\frac{1}{{2y}}$
(C) $\displaystyle 5\sqrt{t}+3$
(D) $\displaystyle \frac{1}{{5x+3}}$

Ans – (A) x² + 5x + 6

2. बहुपद p(x) = 2x + 5 का शून्यक होगा :

(A) $\displaystyle \frac{5}{2}$

(B) $\displaystyle -\frac{5}{2}$

(D) $\displaystyle -\frac{2}{5}$

Ans – (B) $\displaystyle -\frac{5}{2}$

3. निम्नलिखित बीजीय व्यंजकों में से कौन-सा एक बहुपद है ?
(A) y^5/3+6
(B) $\displaystyle \sqrt{y}+5$
(C) $\displaystyle y+\frac{2}{y}$
(D) X³ + 5

Ans – (D) X³ + 5

4. बहुपद 2 – x³ + x⁵+9x⁷ में x³ का गुणांक होगा :
(A) 2
(B) -1
(C) 1
(D) 9

Ans – (B) -1

5. निम्नलिखित बीजीय व्यंजकों में कौन-सा एक बहुपद है?

(A) x^1/4 + 6

(B) $\displaystyle 3{{x}^{2}}+\frac{5}{2}x$

(D) x^3/2 + 2x + 6

Ans – (B) $\displaystyle 3{{x}^{2}}+\frac{5}{2}x$

6. निम्नलिखित बीजीय व्यंजकों में कौन-सा व्यंजक एक बहुपद है ?
(A) $\displaystyle x+\frac{1}{x}$
(B) $\displaystyle \sqrt{x}+3$
(C) $\displaystyle x+\sqrt{3}$
(D) x^1/3 + 6

Ans – (C) $\displaystyle x+\sqrt{3}$

7. बहुपद 2 – y² – y³ + 2y⁸ की घात होगी :
(A) 8
(B) 3
(C) 2
(D) 4

Ans – (A) 8

8. बहुपद 2 – x² + x³ में x² का गुणांक होगा :
(A) 1
(B) -1
(C) 2
(D) 3

Ans – (B) -1

9. बहुपद 5y⁶ – 4y² – 6y + 6 में कितने पर है?
(A) 6
(B) 5
(C) 4
(D) 2

Ans – (C) 4

10. बहुपद p(x) = 2x + 1 का शून्यक होगा :
(A) $\displaystyle -\frac{1}{2}$
(B) $\displaystyle \frac{1}{2}$
(C) 2
(D) 1

Ans – (A) $\displaystyle -\frac{1}{2}$

11. बहुपद t² – 4 का प्रकार है :
(A) द्विपदी
(C) त्रिपदी
(B) एक पदी
(D) इनमें से कोई नहीं

Ans – (A) द्विपदी

12. 5x³ + 4x² + 7x की घात है :
(A) 1
(B) 2
(C) 3
(D) 4

Ans – (C) 3

13. (99)³ का मान है
(A) 970289
(B) 970299
(C) 970389
(D) 970489

Ans -(B) 970299

14. 2x² + 7x + 3 का गुणनखण्ड होगा :
(A) (2x + 1)(x + 3)
(B) (2x + 3)(3x – 2)
(C) (2x – 1)(x + 4)
(D) (2x + 1)(2x – 1)

Ans – (A) (2x + 1)(x + 3)

15. निम्नलिखित में से रिक्त स्थान भरिये (a^m)ⁿ = _________.
(A) a^m+n
(B) a^m-n
(C) a^mn
(D) (mn)^a

Ans – (C) a^mn

16. रिक्त स्थान भरिए (x + y)² = x² + _________ + y²
(A) 3xy
(B) 2x
(C) 2xy
(D) 2y

Ans – (C) 2xy

17. 4y² – 4y+1 का गुणनखण्ड है
(A) (2y + 1)²
(B) (4y – 1)²
(C) (2y – 1)²
(D) (2y-2)²

Ans – (C) (2y – 1)²

18. 27 – 125a³ – 135a + 225a² का गुणनखण्ड है:
(A) (3 + 5a)²
(B) (3a + 5)³
(C) (3a – 5)²
(D) (3 – 5a)³

Ans – (D) (3 – 5a)³

19. यदि x – 1, p(x) = kx² – $\displaystyle \sqrt{2}x$ + 1 का एक गुणनखंड हो, तो k का मान होगा :
(A) $\displaystyle \sqrt{2}+1$
(B) $\displaystyle -1+\sqrt{2}$
(C) $\displaystyle \sqrt{2}-1$
(D) $\displaystyle -\sqrt{2}-1$

Ans – (C) $\displaystyle \sqrt{2}-1$

Chapter 3 – निर्देशांक ज्यामिति

1. बिंदु (6, -7 ) किस चतुर्थांश में स्थित है ?
(A) पहले
(B) दूसरे
(C) तीसरे
(D) चौथे

Ans – (D) चौथे

2. बिन्दु (-1, 3) कार्तीय तल के किस चतुर्थाश में स्थित होगा ?
(A) चतुर्थांश I में
(B) चतुर्थांश II में
(C) चतुर्थांश III मे
(D) चतुर्थांश IV में

Ans – (C) चतुर्थांश III मे

3. x = 2 का आलेख निरूपण :
(A) x – अक्ष के समांतर है
(B) y-अक्ष के समांतर है
(C) मूल बिंदु में से गुजरता है .
(D) कुछ भी नहीं

Ans – (B) y-अक्ष के समांतर है

4. बिन्दु (−1, 4) कौन-से चतुर्थांश में है ?
(A) I
(B) IV
(C) II
(D) III

Ans – (C) II

5. बिन्दु (0, −3) स्थित है ?
(A) x-अक्ष पर
(B) y-अक्ष पर
(C) पहले चतुर्थांश में
(D) दूसरे चतुर्थांश में

Ans – (B) y-अक्ष पर

6. बिंदु (-4, -3) का भुज और कोटि क्या है ?
(A) x = – 4, y = – 3
(B) x = – 2, y = – 4
(C) x = 4, y = 3
(D) कोई नहीं

Ans – (A) x = – 4, y = – 3

Chapter 4 – दो चरो वाले रैखिक समीकरण

1. K का मान होगा, जबकि x = 2, y = 1 समीकरण 2x + 3y = K का एक हल है।
(A) 2
(B) 4
(C) 9
(D) 7

Ans – (D) 7

2. रैखिक समीकरण –2x + 3y = 6 को ax + by + c = 0 के रूप में व्यक्त करके C का मान बताइए
(A) -2
(B) -6
(C) 3
(D) 6

Ans – (B) -6

3. एक नोटबुक की कीमत एक कलम की कीमत से दो गुनी है। इस कथन को निरूपित करने के लिए दो चरों वाला एक रैखिक समीकरण लिखिए।
(A) $\displaystyle \frac{x}{y}+2=0$
(B) x + 2y = 0
(C) 2x + y = 0
(D) x – 2y = 0

Ans – (D) x – 2y = 0

4. निम्नलिखित में समीकरण x – 2y = 4 का हल होगा :
(A) (0, 2)
(B) (0, 4)
(C) (4, 0)
(D) (2, 0)

Ans – (C) (4, 0)

5. दो चरों वाले रैखिक समीकरण के अधिकतम कितने हल होते हैं ?
(A) एक
(B) दो
(C) तीन
(D) अपरिमित रूप से अनेक

Ans – (D) अपरिमित रूप से अनेक

6. समीकरण 6x + 7 तुलना ax + by + c = 0 से करने पर a का मान होगा :
(A) 0
(B) 6
(C) 1
(D) 7

Ans – (B) 6

7. समीकरण x – 2y = 4 का हल है :
(A) (0, 2)
(B) (4, 0)
(C) (1, 1)
(D) (2, 0)

Ans – (B) (4, 0)

8. बिन्दु (4, 1) किस रेखा के समीकरण को संतुष्ट करता है ?
(A) x + 2y = 5
(B) x + 2y = – 6
(C) x + 2y = 6
(D) x + 2y= 16

Ans – (C) x + 2y = 6

9. 4 = 5x – 3y को ax + by + c = 0 के रूप में लिखिए व c का मान बताइए :
(A) 5
(B) -3
(C) 0
(D) -4

Ans – (D) -4

10. यदि बिंद (2, 1) समीकरण 2x + 3 = k के आलेख पर स्थित हो तो k का मान होगा :
(A) 8
(B) 6
(C) 7
(D) -7

Ans – (C) 7

Chapter 5 – यूक्लिड की ज्यामिति का परिचय

NO MCQ

Chapter 6 – रेखाएं और कोण

1. दिए हुए दो भिन्न बिन्दुओं से होकर कितनी रेखाएं खीची जा सकती हैं ?
(A) एक अद्वितीय
(B) दो
(C) अनेक
(D) कोई नहीं

Ans – (A) एक अद्वितीय

2. दो कोणों का योग 180° हो, तो ऐसे कोण कहलाते हैं:
(A) न्यून कोण
(B) पूरक कोण
(C) संपूरक कोण
(D) प्रतिवर्ती कोण

Ans – (C) संपूरक कोण

3. नीचे दिए कथनों में कौन-सा असत्य है ?
(A) दो भिन्न रेखाओं में एक से अधिक बिंदु उभयनिष्ठ नहीं हो सकती।
(B) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है।
(C) एक बिंदु से होकर केवल एक ही रेखा खींची जा सकती है।
(D) यदि दो वृत्त बराबर हैं तो उनकी त्रिज्याएँ बराबर होती हैं।

Ans – (C) एक बिंदु से होकर केवल एक ही रेखा खींची जा सकती है।

4. यदि a || b, b || c तो कौन-सा कथन सत्य है ?.
(A) a ⊥ c
(B) a ⊥ b
(C) a || c
(D) b ⊥ c

Ans – (C) a || c

5. यदि A, B और C एक रेखा पर स्थित तीन बिंदु हों और B बिंदु A और C के मध्य स्थित हो, तो कौन-सा कथन सत्य है ?
(A) AB + BC = AC
(B) AB – BC = AC
(C) AB+ AC = BC
(D) AB+ BC = AB

Ans – (A) AB + BC = AC

6. एक रेखा का वह भाग जिसके दो अंत बिन्दु हों, कहलाता है :
(A) रेखा
(B) किरण
(C) रेखाखण्ड
(D) शीर्ष

Ans – (C) रेखाखण्ड

7. शीर्षाभिमुख कोण बराबर होते हैं, यदि दो रेखाएँ परस्पर ___________ हो।
(A) प्रतिच्छेदी
(B) समान्तर
(C) लंब
(D) इनमें से कोई नहीं

Ans – (A) प्रतिच्छेदी

8. एक न्यून कोण का माप होता है
(A) 0° से 90° के बीच
(B) 90° से 180″ के बीच
(C) 180° से 270 के बीच
(D) 270° के ऊपर

Ans – (A) 0° से 90° के बीच

9. यदि एक किरण एक रेखा पर खड़ी हो, तो इस प्रकार बने आसन्न कोणों का योग होता है :
(A) 360°
(B) 180°
(C) 120°
(D) 90°

Ans – (B) 180°

10. आकृति में x का मान होगा।

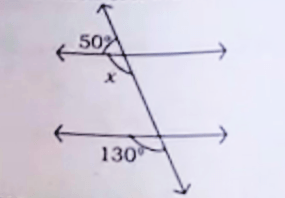
(A) 50°
(B) 100°
(C) 130°
(D) 60°

Ans – (C) 130°

11. आकृति में, x का मान होगा :

(A) 9°
(B) 18°
(C) 27°
(D) 36°

Ans – (A) 9°

Chapter 7 – त्रिभुज

1. “दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की दो भुजाएँ और उनका अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अंतर्गत कोण के बराबर हों।” यह निम्नलिखित में से सर्वांगसमता का कौन-सा नियम है ?
(A) AAS
(B) ASA
(C) SAS
(D) SSS

Ans – (C) SAS

2. किसी त्रिभुज की ऊँचाई और आधार क्रमशः 8 cm व 3 cm हैं, उसका क्षेत्रफल होगा :
(A) 24 cm
(B) 12 cm
(C) 12 cm²
(D) 24 cm²

Ans – (C) 12 cm²

3. किसी त्रिभुज की दो भुजाएँ क्रमशः 60 सेमी० और 100 सेमी ० हैं। इसका परिमाप 300 सेमी ० है, तो तीसरी भुजा होगी :
(A) 60 सेमी ०
(B) 100 सेमी ०
(C) 140 सेमी ०
(D) 40 सेमी ०

Ans – (C) 140 सेमी ०

4. “यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।” निम्नलिखित में यह सर्वांगसमता के किस नियम का पालन करता है ? 1
(A) SAS
(B) RHS
(C) ASA
(D) AAS

Ans – (B) RHS

5. किसी त्रिभुज की ऊँचाई 10 सेमी और आधार 5 सेमी है, उसका क्षेत्रफल होगा :
(A) 50 सेमी²
(B) 25 सेमी²
(C) 15 सेमी²
(D) 20 सेमी²

Ans – (B) 25 सेमी²

6. प्रत्येक कोण समकोण नहीं होता है :
(A) आयत का
(B) वर्ग का
(C) त्रिभुज का
(D) घन का

Ans – (C) त्रिभुज का

7. त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से होता है।
(A) छोटा
(B) बड़ा
(C) बराबर
(D) इनमें से कोई नहीं

Ans – (B) बड़ा

8. किसी त्रिभुज के तीनों कोणों का योग होता है
(A) 120°
(B) 180°
(C) 270°
(D) 360°

Ans – (B) 180°

9. किसी समकोण त्रिभुज का क्षेत्रफल होता है :

(A) $\displaystyle \frac{1}{2}$ x आधार × ऊँचाई

(B) 2 x आधार x ऊँचाई

(D) 3 x आधार x ऊँचाई

Ans – (A) $\displaystyle \frac{1}{2}$ x आधार × ऊँचाई

10. यदि a, b और c त्रिभुज की भुजाएँ हैं। त्रिभुज का अर्थ-परिमाप होगा :

(A) $\displaystyle S=\frac{{a+b-c}}{2}$

(B) $\displaystyle S=\frac{{a-b-c}}{2}$

(D) $\displaystyle S=\frac{{a+b+c}}{3}$

Ans – (C) $\displaystyle S=\frac{{a+b+c}}{2}$

11. यदि M, समकोण ΔABC के कर्ण AC का मध्य बिन्दु हो, तो BM = $\displaystyle \frac{1}{2}$ :
(A) AC
(B) AB
(C) BC
(D) इनमें से कोई नहीं

Ans – (A) AC

12. सेट स्क्वायर के युग्म में एक त्रिभुज के कोण होते हैं :
(A) 30°, 40°, 100°
(B) 60°, 30°, 90°
(C) 30°, 30°, 45°
(D) कोई भी नहीं

Ans – (B) 60°, 30°, 90°

13. एक त्रिभुज जिसकी दो भुजाएँ 8 सेमी और 11 सेमी हैं और जिसका परिमाप 32 सेमी है। उसका अर्धपरिमाप होगा : 1
(A) 4 सेमी
(B) 13 सेमी
(C) 14 सेमी
(D) 16 सेमी

Ans – (D) 16 सेमी

14. एक त्रिभुजाकार भूखंड की भुजाओं का अनुपात 3: 5: 7 है और उसका परिमाप 300 मी० है। उस भूखंड का क्षेत्रफल होगा : 1
(A) 1500 $\displaystyle \sqrt{3}$ मी²
(B) 1200 $\displaystyle \sqrt{3}$ मी²
(C) 1800 $\displaystyle \sqrt{3}$ मी²
(D) 1600 $\displaystyle \sqrt{3}$ मी²

Ans – (A) 1500 $\displaystyle \sqrt{3}$ मी²

15. एक समद्विबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm लम्बाई की हैं। इस त्रिभुज का क्षेत्रफल होगा :
(A) $\displaystyle 8\sqrt{{15}}$ cm²
(B) $\displaystyle 7\sqrt{{12}}$ cm²
(C) $\displaystyle 9\sqrt{{15}}$ cm²
(D) $\displaystyle 15\sqrt{{15}}$ cm²

Ans – (C) $\displaystyle 9\sqrt{{15}}$ cm²

16. आकृति में यदि QT ⊥ PR, ∠TQR = 40° ∠SPR = 30° है, तो y का मान होगा :

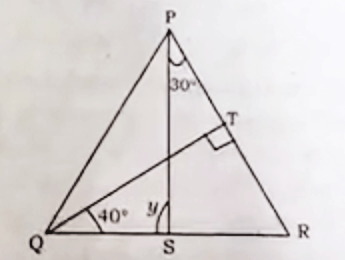
(A) 80°
(B) 70°
(C) 30°
(D) 40°

Ans – (A) 80°

Chapter 8 – चतुर्भुज

1. बिन्दुओं (0, 0), (0, 2), (2, 2) और (2, 0) को मिलाने पर कौन-सी आकृति प्राप्त होती है ?
(A) वर्ग
(B) आयत
(C) समचतुर्भुज
(D) समांतर चतुर्भुज

Ans – (A) वर्ग

2. यदि किसी चतुर्भुज के विकर्ण परस्पर समकोण पर प्रतिच्छेद करें, तो यह आकृति क्या होगी?
(A) समांतर चतुर्भुज
(B) वर्ग
(C) सम चतुर्भुज
(D) समलंब चतुर्भुज

Ans – (C) सम चतुर्भुज

3. एक समचतुर्भुज के कोण यदि 3 : 4 : 5 : 6 के अनुपात में हो, तो चतुर्भुज के कोण क्रमशः क्या होंगे ?
(A) 60°, 80°, 100°, 120°
(B) 120°, 100°, 80°, 60°
(C) 120°, 60°, 80°, 100°
(D) 80°, 100°, 120°, 60°

Ans – (A) 60°, 80°, 100°, 120°

Chapter 9 – वृत्त

1. अर्धवृत्त का कोण होता है :
(A) पूरक कोण
(B) अधिक कोण
(C) समकोण
(D) न्यून कोण

Ans – (C) समकोण

2. संपूर्ण वृत्त की लंबाई को कहते हैं।
(A) व्यास
(B) परिचि
(C) त्रिज्या
(D) चाप

Ans – (B) परिचि

3. कितने असंरेख बिंदुओं में से केवल एक ही वृत्त खींचा जा सकता है ?
(A) तीन
(B) चार
(C) पाँच
(D) छ:

Ans – (A) तीन

4. वृत्त का केन्द्र वृत्त के ________ में स्थित होता है।
(A) बहिर्भाग
(B) परिचि
(C) अभ्यन्तर
(D) परिमाप

Ans – (C) अभ्यन्तर

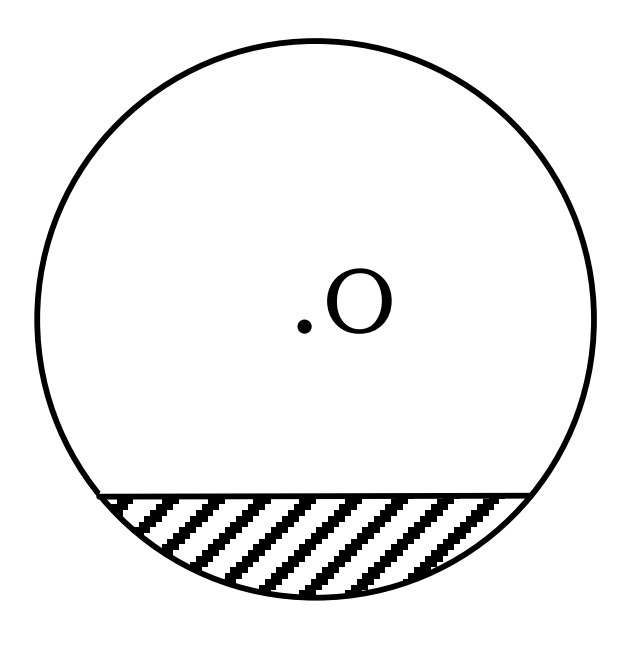
5. आकृति में, वृत्त के छायांकित भाग को कहते हैं:

(A) दीर्घ त्रिज्याखंड
(B) दीर्घ वृत्तखंड
(C) लघु त्रिज्याखंड
(D) लघु वृत्तखंड

Ans – (D) लघु वृत्तखंड

Chapter 10 – हीरोन का सूत्र

NO MCQ

Chapter 11 – पृष्ठीय क्षेत्रफल और आयतन

1. एक लंबवृत्तीय शंकु का वक पृष्ठीय क्षेत्रफल क्या है जिसकी तिर्यक ऊँचाई 10 सेमी है और आधार की त्रिज्या 7 सेमी है ?
(A) 220 सेमी²
(B) 110 सेमी³
(C) 132 सेमी³
(D) 232 सेमी³

Ans – (A) 220 सेमी²

2. लंब वृत्तीय शंकु का आयतन होगा जिसकी त्रिज्या 7 सेमी व ऊँचाई 3 सेमी हो :
(A) 154 सेमी³
(B) 154 सेमी³
(C) 282 सेमी²
(D) 284 सेमी

Ans – (A) 154 सेमी³

3. एक लंबवृत्तीय शंकु के आधार की त्रिज्या 11.3 सेमी है और इसका वक्रपृष्ठ 355 सेमी² है। इस शंकु की ऊँचाई होगी : ( $\displaystyle \pi =\frac{{355}}{{113}}$ लीजिए)
(A) 11 सेमी
(B) 9 सेमी
(C) 5 सेमी
(D) 10 सेमी

Ans – wrong options

4. 14 cm व्यास वाले गोले का पृष्ठीय क्षेत्रफल होगा:
(A) 28 cm
(B) 28 cm²
(C) 42 cm²
(D) 616 cm²

Ans – (D) 616 cm²

5. त्रिज्या वाले गोले का आयतन होगा :
(A) 4πr
(B) 4πr²

(D) $\displaystyle \frac{4}{3}\pi {{r}^{3}}$

Ans – (D) $\displaystyle \frac{4}{3}\pi {{r}^{3}}$

6. एक गोले का आयतन 524 सेमी³ है। इस गोले का व्यास होगा :
(A) 4 सेमी
(B) 5 सेमी
(C) 3 सेमी
(D) 6 सेमी

Ans – wrong options

7. एक अर्थगोले जिसकी त्रिज्या r है, का वक्र पृष्ठीय क्षेत्रफल होता है :
(A) 4πr²
(B) 3πr²
(C) 2πr²
(D) $\displaystyle \frac{4}{3}$

Ans – (C) 2πr²

Chapter 12 – सांख्यिकी

1. 10, 7, 13, 20, 15 का माध्य होगा :
(A) 12
(B) 13
(C) 10
(D) 15

Ans – (B) 13

2. किसी वर्ग-अन्तराल 180-190 का वर्ग चिह्न होगा।
(A) 185
(B) 180
(C) 190
(D) 370

Ans – (A) 185

3. प्रथम पाँच प्राकृतिक संख्याओं का माध्य होगा :
(A) 5
(B) 3
(C) 4
(D) 2

Ans – (B) 3

4. आँकड़ों के अधिकतम और न्यूनतम मानों के अंतर को कहते हैं।
(A) माध्य
(B) माध्यक
(C) परिसर
(D) बहुलक

Ans – (C) परिसर

5. वर्ग अंतराल 20 – 30 में उपरि वर्ग सीमा क्या है ?
(A) 50
(B) 20
(C) 10
(D) 30

Ans – (D) 30

6. आँकड़ों 40, 20, 36, 60, 56, 88, 50, 80 का परिसर होगा :
(A) 40
(B) 68
(C) 56
(D) 88

Ans – (B) 68

7. वर्ग 150-160 का वर्ग चिह्न है :
(A) 145
(B) 310
(C) 10
(D) 155

Ans – (D) 155

8. किसी वर्ग अंतराल का वर्ग चिह्न होता है :

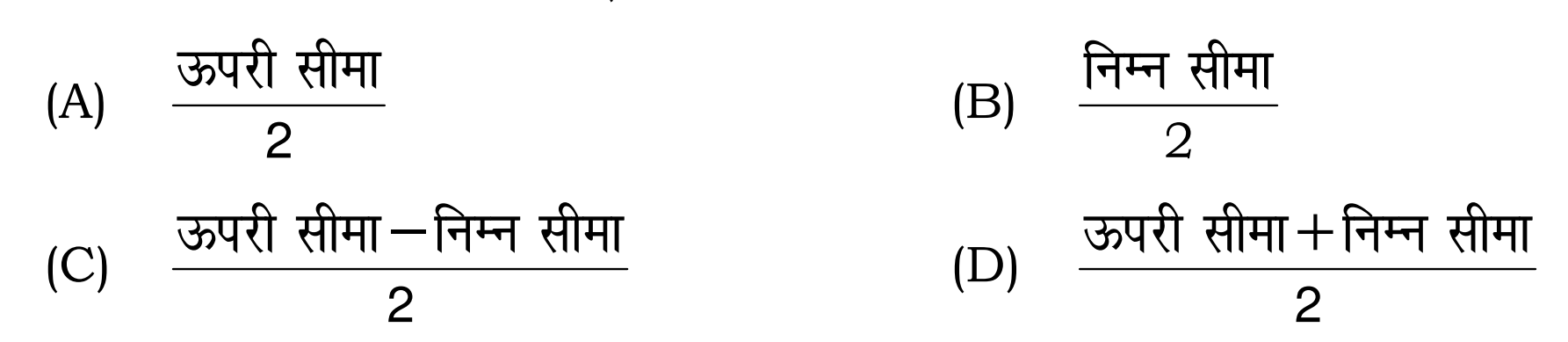
Ans – (D)

9. किसी कक्षा के 20 विद्यार्थियों के अंक (10 में से) निम्नलिखित है :

9, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9

बहुलक अंक क्या है ?

(A) 7
(B) 9
(C) 3
(D) 10

Ans – (B) 9

10. किसी कक्षा के 9 विद्यार्थियों की ऊँचाई (सेमी में) दी गई है :

155, 160, 145, 149, 150, 147, 152, 144, 148

इन आंकड़ों का माध्यक है:

(A) 150
(B) 147
(C) 149
(D) 148

Ans – (C) 149