HBSE Class 9 Math Important Question Answer 2026

Most of students search over Google for Haryana Board (HBSE) Important Questions 2026. Here is the Main reason because HBSE Board Says that in HBSE Exam 2026 (last 3 Years of Questions will Repeat) so that here are the selected List of Questions of Haryana Board For Class 12.

HBSE Class 9 Math Important Question Answer 2026

Chapter 1 – Number System

Q1. The $\displaystyle \frac{p}{q}$ form of $\displaystyle 0.\overline{{47}}$ is _______ .

Q2. Rationalise the denominator of $\displaystyle \frac{1}{{7+3\sqrt{2}}}$ .

Q3. Rationalize the denominator of $\displaystyle \frac{5}{{\sqrt{3}-\sqrt{5}}}$

Q4. What will be get after rationalize the denominator of $\displaystyle \frac{1}{{\sqrt{5}+\sqrt{2}}}$ ?

Q5. The value of $\displaystyle (3+\sqrt{3})(2+\sqrt{2})$ is

Q6. Find one rational number between 3 and 4.

Q7. Every rational number is an integer. (True/False)

Q8. Simplify: $\displaystyle (3+\sqrt{3})(3-\sqrt{3})$

Q9. Simplify : $\displaystyle {{2}^{{\frac{2}{3}}}}{{.2}^{{\frac{1}{5}}}}$

Q10. Express 0.3333…….= $\displaystyle 0.\overline{3}$ in the form $\displaystyle \frac{p}{q}$ , where p and q are integers and q ≠ 0.

Q11. Express 0.99999 _______ in the form $\displaystyle \frac{p}{q}$

Q12. Express $\displaystyle 0.\overline{6}$ in the form $\displaystyle \frac{p}{q}$ , where p and q are integers and q≠ 0.

Chapter 2 – Polynomials

Q1. Factorize the quadratic polynomial 6x² + 5x – 6 .

Q2. Factorize : 27x³ + y³ + z³ – 9xyz Most Important

Q3. Factorise : 64m³ – 343m³

Q4. Factorise : $\displaystyle \frac{{{{x}^{2}}}}{{100}}-{{y}^{2}}$

Q5. Factorise: 8a³ + b³ + 12a²b + 6ab²Most Important

Q6. Evaluate 103 x 107 without direct multiplication.

Q7. Factorize: 4x² + 9y² + 16z² + 12xy – 24yz – 16xz

Q8. Factorise : x³ + 13x² + 32x + 20

Q9. Factorise: x³ – 2x² – x + 2

Q10. Evaluate 103 x 107 by using identity.

Q11. Without actually calculating the cubes, find the value of (28)³ + (−15)³ + (−13)³.

Q12. Using suitable identity, find the value of (102)².

Q13. Find the value of k for which x – 1 is a factor of the polynomial x² + x + k .

Q14. Zero of p(x) = 3x + 1 is :

Q15. The coefficient of x² in 2 – x² +x³ is _________ .

Q16. The factors of 64m³ – 343n³ are __________.

Q17. What is product of ( x + 4 ) (x + 10) ?

Ans – x² + 14x + 40

Q18. Write $\displaystyle {{[x-\frac{2}{3}y]}^{{-3}}}$ in expanded form.

Q19. Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k

Q20. Find the value of k, if x – 1 is a factor of P(x), P(x) = 2x² + kx + √2

Q21. Use the factor theorem factorize of x² – 5x + 6 .

Q22. Factorize: 2x² + 7x + 3

Q23. Factorize: 64x³– 343y³

Q24. Factorize: 8x³ + y³ + 27z³ – 18xyz

Chapter 3 – Coordinate Geometry

Q1. In which quadrant or on which axis do each of the points (-2, 4), (3, -1), (-1, 0), (1, 2) lie? Verify your answer by locating them on the Cartesian plane.

Q2. Plot the following ordered pairs (x, y) of numbers as points in the Cartesian Plane:

x	-2	-3	3	0
y	-3	7	-1	-1.5

Q3. Plot the following ordered pairs of numbers as points on the Cartesian Plane :

x	3	-2	-1	1
y	-1	6	-4	-3

Q4. What is the name of each part of the plane formed by horizontal and the vertical lines in the Cartesian plane?

Q5. Point (5, -7) lies in which Quadrant ?

Q6. The point (0, 0) where x-axis and y-axis intersect is called _________ .

Q7. The abscissa and coordinate of (6, −4 ) is ________.

Q8. From the fig given below :

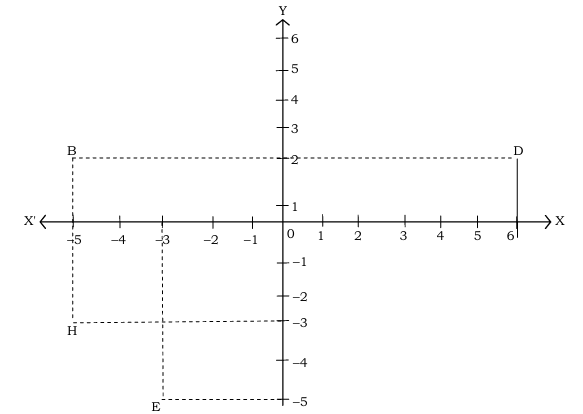
Write the answer of each of following from figure:

(i) The coordinates of B

(ii) The point identified by the coordinates (-3, -5)

(iii) The abscissa of the point D

(iv) The coordinate of point H

Q9.

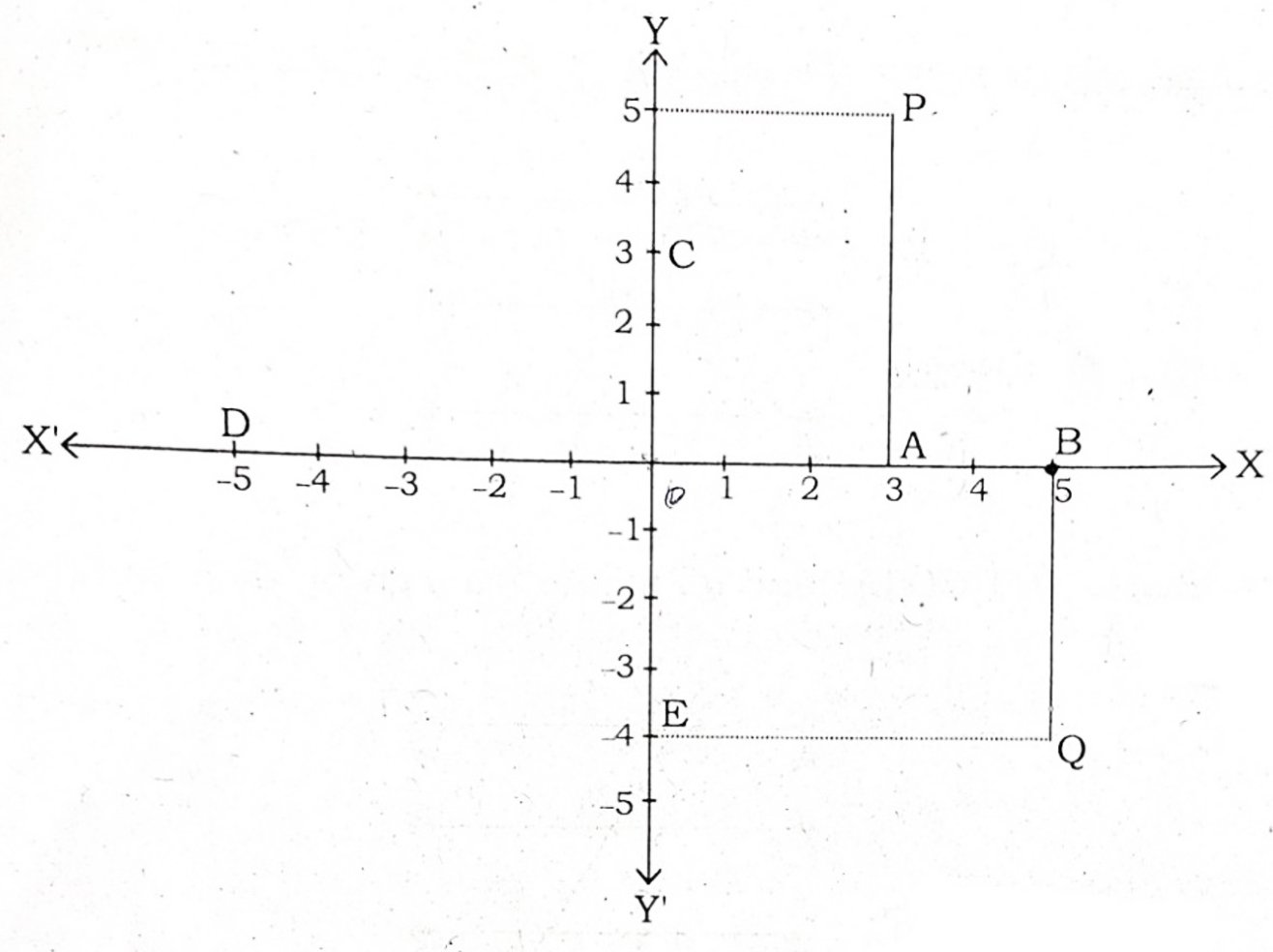
Look at the above figure and answer the following:
(i) Coordinates of A, B, C, D, E

(ii) Abscissa of point D

(iii) Ordinate of point E

(iv) Coordinates of point P, Q

Chapter 4 – Linear Equations in Two Variables

Q1. Find the four solutions for the equation 2x + y = 7 .

Q2. The floor of a rectangular hall has the perimeter 250 m. If the cost of the painting the four walls at the rate ₹ 12 per m² is ₹ 18,000, find the height of the hall.

Q3. What is solution of (2x + 1) = x + 3

Q4. Solve the equation 2x + 1 = x – 3 and represent the solution on (i) The number line, (ii) The Cartesian plane.

Q5. Solve the equation 2x + 8 = 0 and represent the solution on (i) the number line (ii) the Cartesian plane.

Q6. Find four different solutions of the equation x+2y = 6.

Q7. Find the value of P if x = 2 , y = 1 is a solution of the equation 2x + 3y = P

Q8. The solution of a linear equation is not affected when the same number is added or subtracted from both the sides of the equation. (True/False)

Ans – True

Chapter 5 – Introduction to Euclid’s Geometry

Q1. What is second postulate of Euclid ?

Q2. Write the first postulate of Euclid.

Ans – A straight line may be drawn from any one point to any other point.

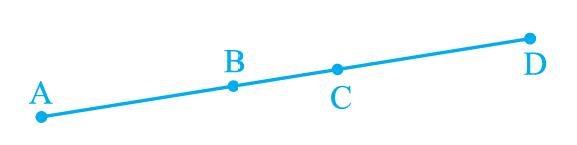
Q3. If in figure AC = BD, then prove that AB = CD : Most Important

Chapter 6 – Lines and Angles

Q1. Write the name of the point where these two lines intersect.

Q2. Give a definition for each of the following terms:
(i) Parallel lines.
(ii) Line segment

Q3. Define supplementary angle. Give its two examples also.

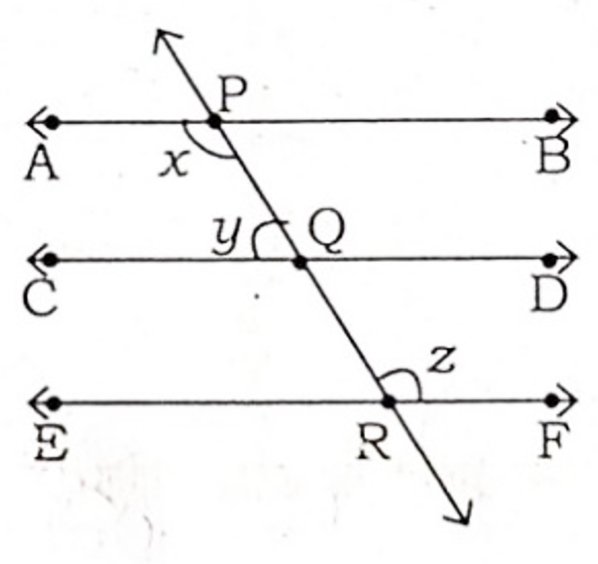
Q4. In the given figure, AB || CD || EF and y: z = 3 : 7 are given, then find the value of x.

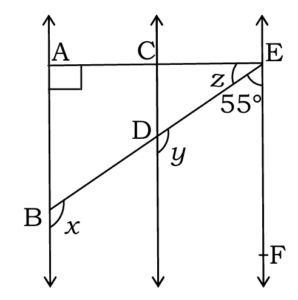
Q5. In fig., AB || CD and CD || EF. And EA ⊥ AB. If ∠BEF 55° then find the values of x, y and z.

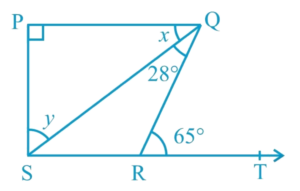
Q6. In fig., if PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°. Then find the values of x and y.

Q7. A terminated line can be produced indefinitely. (True / False )

Chapter 7 – Triangles

Q1. Prove that angles opposite to equal sides of an isosceles triangle are equal.

Q2. Show that the angles of an equilateral triangle are 60° each. Most Important

Q3. Construct a triangle ABC in which BC = 8cm, ∠B = 45° and AB – AC = 3.5 cm. Most Important

Q4. ABC is a triangle right angled at C. A line through the mid point M of hypotenuse AB and parallel to BC intersects AC at D. Show that:

(i) D is the mid point of AC

(ii) MDIAC

(iii) CM = MA = $\displaystyle \frac{1}{2}$ AB

Q5. Construct a triangle ABC in which BC = 7 cm, ∠B – 75° and AB + AC = 13 cm. Most Important

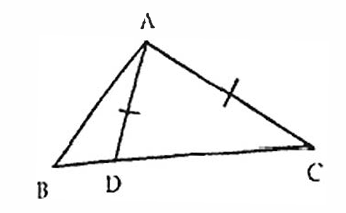
Q6. D is a point on side BC of ΔABC such that AD = AC in given figure show that AB > AD.

Q7. ΔABC is a right angled triangle in which ∠A = 90° and AB = AC. What is the value of ∠B and ∠C?

Q8. If ΔPRQ ≅ ΔCBA , then find:

(i) QR =…,.

(ii) PR =……

(iii) PO = …..

(iv) ∠B =…….

Q9. The triangle formed by joining the mid-points of the sides of an isosceles triangle is ________.

Q10. Construct a triangle ABC in which ∠B = 60°, ∠C = 45° and perimeter is 10 cm.

Q11. To construct a triangle we must know at least its ________ parts .

Q12. The sum of any two sides of a triangle is _______ than the third side.

Chapter 8 – Quadrilaterals

Q1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Q2. Show that the diagonals of a rhombus are perpendicular to each other. Most Important

Q3. ABCD is a quadrilateral in which P, Q, R and S are mid points of the sides AB, BC, CD and DA. AC is a diagonal, show that:

(i) SR || AC and SR= $\displaystyle \frac{1}{2}$ AC

(ii) PQ = SR

(iii) PORS is a parallelogram

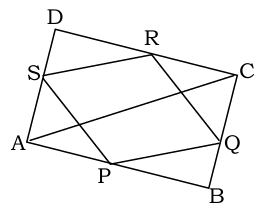
Q4. If two sides of a cyclic quadrilateral are parallel, prove that:

(i) remaining two sides are equal and

(ii) both diagonals are equal

Q5. Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.

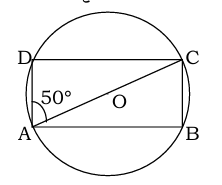
Q6. In cyclic quadrilateral ABCD, AOC is the diameter of circle. Ir ∠CAD = 50°, then ∠ACD is :

Q7. The diagonals of a rectangle are _______ .

Q8. If diagonal of a quadrilateral bisect each other, then quadrilateral is parallelogram. (True/False

Chapter 9 – Circles

Q1. Prove that a cyclic parallelogram is a rectangle.

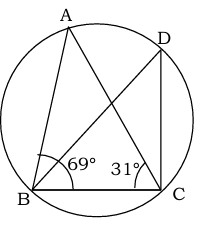
Q2. In figure angle ∠ABC = 69° and angle ∠ACB =31° find ∠BDC. Most important

Q3. A Roller 120 cm long has a diameter 84 cm. To level a playground, it takes 500 complete revolutions. Determine the area of playground in m² .

Q4. Angles in the same segment of a circle are ______ .

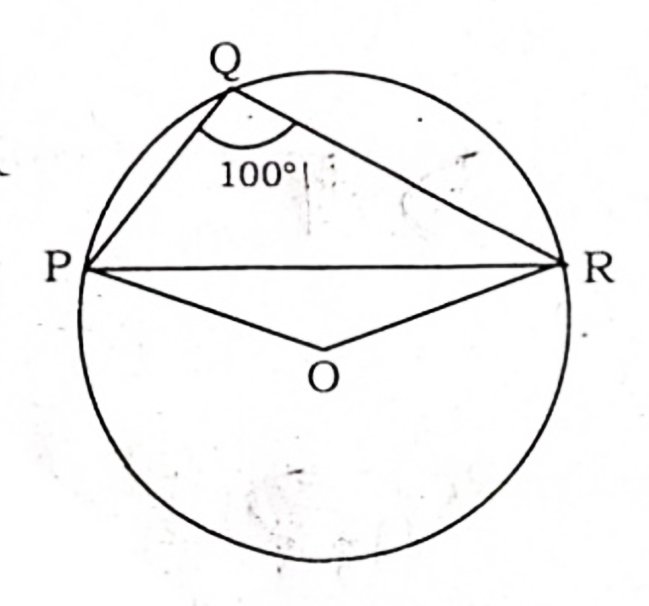
Q5. In the given figure ∠PQR = 100° , where P, Q and R are points on a circle with centre O. Find ∠OPR .

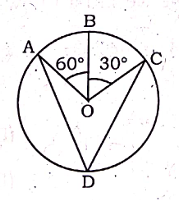
Q6. In fig., A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the are ABC, then ∠ADC will be:

Q7. A circle has only finite numbers of equal chords. (True/False)

Ans – False

Chapter 10 – Heron’s Formula

Q1. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.

Q2. Sides of a triangle are in the ratio of 3 : 5 : 7 and its perimeter is 300 cm. Find its area.

Chapter 11 – Surface Areas and Volumes

Q1. Find the volume of right circular cone with radius 6 cm and height 7 cm. Most Important

Q2. The height of a cone is 15 cm. If its volume is 1570 cm³. the radius of it base is ?

Q3. The volume of a right circular cone is 9856 cm³. If the diameter of the base is 28 cm. Find :
(i) Height of the cone
(ii) Slant height of the cone
(iii) Curved surface area of the cone

Q4. A conical tent is 10 m high and the radius of its base is 24 m. Find:

(i) Slant height of the tent.

(ii) Cost of the canvas required to make the tent, if the cost of 1 m² canvas is ₹ 70.

Q5. The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find:

(i) Its inner curved surface area.

(ii) The cost of plastering this curved surface at the rate of Rs. 40 per m².

Q6. Volume of a hemisphere with radius r will be ________ .

Q7. Find the total surface area of a hemisphere if its radius is 21 cm

Q8. Find the radius of a sphere whose surface area is 154 cm².

Chapter 12 – Statistics

Q1. The following table gives the lifetimes of 400 neon lamps :

Lifetimes ( In Hours )

Number of Lamps

300-400

400-500

500-600

600-700

700-800

800-900

900-1000

(i) Represent the given information with the help of a histogram.

(ii) How many lamps have a lifetime of more than 700 hours?

Q2. The Blood Groups of 30 students of class IX are recorded as follows:

A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O

Represent this data in the form of a frequency distribution table.

Q3. A family with a monthly income of 6,400 plans his budget for a month as given below :

Grocery	Clothing	Education	Miscellaneous	Savings
2100	600	1200	1500	1000

(i) Represent the above data by a bar-graph.

(ii) On which item they spent more?

Q4. Class mark of class 140-150 is _________.